코로나19가 수도권을 넘어 전국적으로 퍼져나가는 중에 8월 31일 일일 신규 확진자 수는 200명대 중반을 나타냈습니다. 신종 코로나 확산 우려 속에 수도권 학교들의 원격수업이 결정되었습니다. 앞으로 감염자 수가 더 늘어날 것이다, 줄어들 것이다, 지난 주말이 분수령이다 등등 여러 가지 예측과 추측들이 쏟아지는 실정입니다.

 | 수학적 모델링

그런데 각 기관에서 질병의 확산을 어떻게 예측하고 있는 것일까요? 여기엔 여러 수학적 모델이 적용되고 있다는 사실을 알고 있나요? 다 함께 수학 교과서를 펼쳐 확인해 봅시다! 복잡한 실제상황을 단순하고 명료하게 바꿔 현상을 이해하는 것을 ‘모델링’이라고 합니다.

실제로는 상당히 복잡하고 여러 변수를 가지고 있는 아프리카 밀림의 생태계를 떠올려 봅시다. 이 생태계를 아주 단순하게 설명해 보자면, 생산자(식물) - 1차소비자(초식동물) - 2차소비자(육식동물)의 구성으로 이야기할 수 있습니다. 여기에 점점 독립영양생물, 종속영양생물, 분해자, 3차소비자, 무기물, 여러 환경 요소 등을 덧붙여 나가면 실제 아프리카 생태계에 점점 가까워 지겠죠.

위 구성원들의 상관관계를 수학적 수식과 함수로 기술하면 아프리카 생태계에 대한 수학모델이 완성됩니다. 신종 코로나의 증감 추이도 여러 가지 수학적 모델로 설명이 가능합니다. 전문영역으로 들어가면 상당한 수준의 통계와 미적분 이론이 필요합니다만, 교과서 수준으로 우리가 이해할 만한 수학적 모델을 만들어 봅시다. 우리는 고등학교 2학년 때 ‘수열’ 단원을 배웁니다. 그리고 12세기 이탈리아의 수학자 피보나치는 ‘피보나치 수열’을 통해 자연상태 토끼의 개체수를 모델링했습니다. 다음과 같은 고민에 대한 해답을 냈던 것이죠.

| 토끼 개체수에 대한 피보나치의 수학적 모델링

 

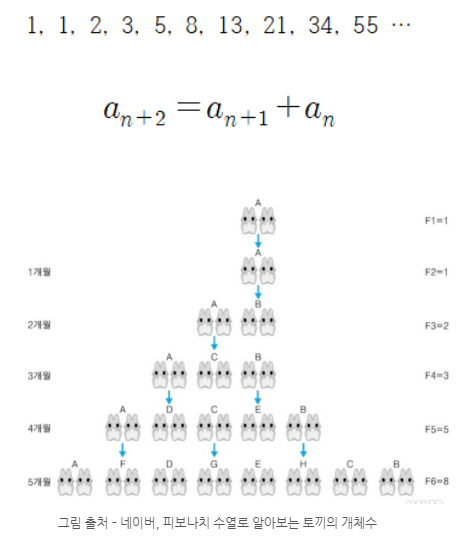
그러나 토끼 개체수에 대한 피보나치의 수학적 모델링에는 한계가 있습니다. 바로 토끼들의 수명이 빠졌기 때문이죠. 뿐만 아니라 먹을 수 있는 풀의 양, 포식자, 질병, 자연도태 등의 여러 환경 요소들도 빠졌습니다. 그러나 기본적인 피보나치의 수열에 위에 열거한 환경 요인들을 수식으로 붙여 나가면 실제 토끼 개체수의 증감과 꽤 비슷한 모델을 얻을 수 있습니다.

 

 | 일상에 수열 접목하기

신종 코로나에도 비슷한 작업을 할 수 있습니다. 접촉자 간의 평균 감염률을 바탕으로 피보나치 수열과 비슷한 단순한 점화식을 만들어 낼 수 있는 것이죠. 여기에 실제와 비슷한 여러 외부 요인들을 첨가합니다.

 

감염자 1인당 평균 접촉자의 수, 감염률, 잠복기, 감염군, 회복군, 치명율 등등의 의학 요인들을 수식화 하여 거대한 모델링 함수를 만들어 나가는 것입니다. 사실, 수학적 모델은 사회 다방면에서 쓰이고 있습니다. 의학이나 이공계 분야 뿐만 아니라, 사회과학과 인문과학에서도 현상의 이해나 실제에 적용을 목적으로 수학적 모델을 다루고 있습니다. 각 분야의 시뮬레이션들이 대부분 수학적 모델링이라 생각할 수 있습니다. 이런 수학적 모델 중 우리에게 친숙한 수열이 사용되기도 하구요. 코로나나 사회현상 등에 대한 여러 예측들이 조금씩 다른 이유는 각자가 고안해 낸 수학적 모델링이 다 다르기 때문입니다.

 

우리는 고3까지 여러 종류의 수열과 함수를 배웁니다. 이 중 코로나 수학모델에 적합한 수식은 무엇일까요? 여러가지 점화식? 지수함수? 로그함수? 이항분포? 오늘 한 번 고민해 보고 탐구해 봅시다. 교과서 속 수학을 좀 더 우리 일상으로 끌어당겨 봅시다!