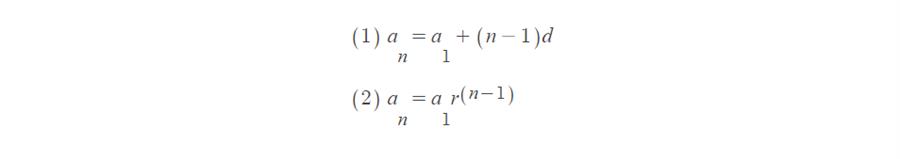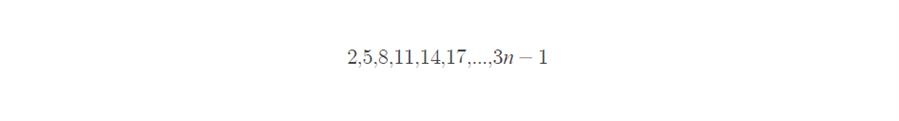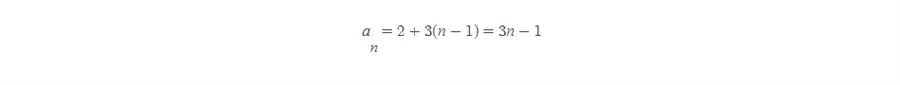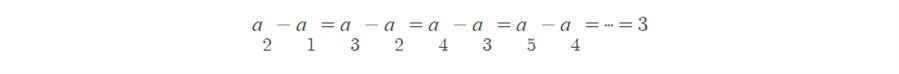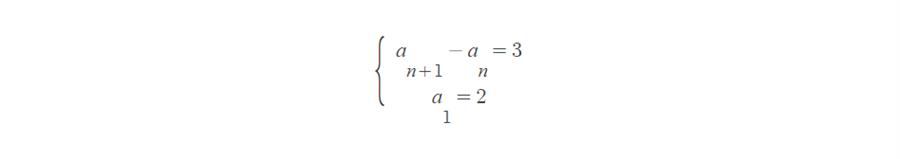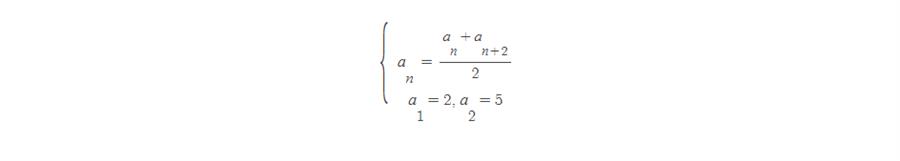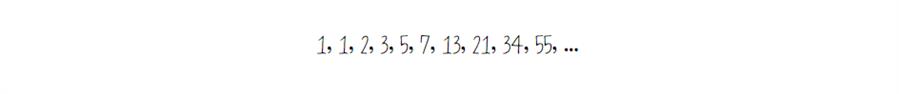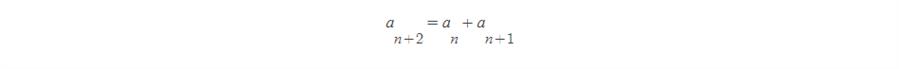1학기 기말고사가 코앞으로 다가왔습니다. 이제 2학년 학생들은 수 1의 마지막 단원 ‘수열의 귀납적 정의’를 배우고 있습니다. 어찌 되었든 등차수열 · 등비수열 · 수열의 합까지는 힘겹게 버텼는데, ‘수열의 귀납적 정의’부터는 공부를 내려놓는 학생들이 꽤 발생합니다. 도대체 이게 뭐 그리 대단한 내용이라고, 포기하는 사람들까지 유발하는 걸까요? 가장 근본적인 부분부터 점검해 봅시다.

현장에 나가보면 이 간단한 물음에 답하지 못하는 학생들이 절반 가까이 됩니다. 게다가 점화식이 무엇인지까지 물으면 더 많은 학생들이 입을 다뭅니다. 수열의 귀납적 정의에 대한 개념부터 세우지 못한 학생들이 많다는 뜻입니다. 이 이전까지 우리는 수열을 일반항으로 정의했습니다. 일정한 수가 계속 더해지는 등차수열은 ①식처럼, 일정한 수가 계속 곱해지는 등비수열은 ②식처럼 말이죠. 이렇게 우리는 문자 n으로 만들어진 일반항으로 수열을 정의하는 데 익숙했습니다.
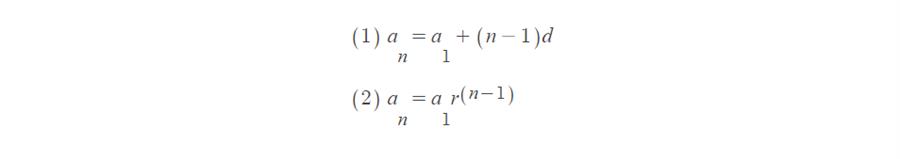
하지만 동일한 등차수열을 일반항이 아닌, 다른 방식으로도 표현할 수 있습니다. 다음의 등차수열을 생각해 해 봅시다.
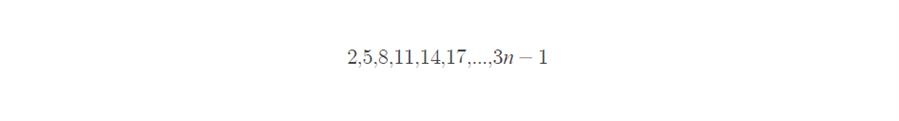
우리는 위 식을 보고 등차수열 일반항을 바로 떠올릴 수 있습니다.
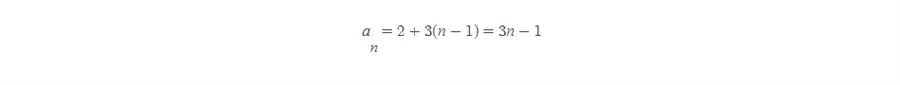
그러나 일반항 말고 다음과 같은 식으로 표현할 수도 있지요.
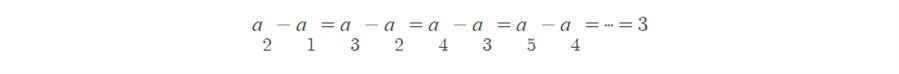
즉 이웃한 두 항의 차가 언제나 3이란 뜻입니다. 이것을 일반화하면 다음과 같은 표현이 가능합니다.
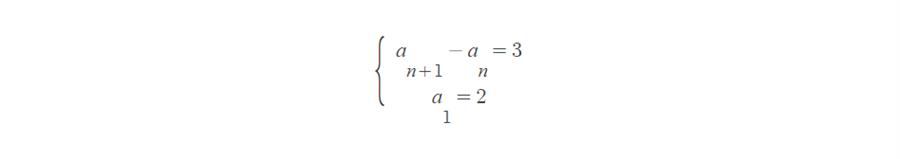
이렇게 일반항이 아닌 이웃한 항들의 관계로 수열을 설명하는 방식을 수열의 귀납적 정의라고 합니다. 그리고 ‘수열의 귀납적 정의’에서 사용된 수열의 관계식을 ‘점화식’이라고 부릅니다. ‘수열의 귀납적 정의’는 같은 수열도 여러 가지 다양한 방식으로 표현 가능합니다. 위에 적어 놓은 등차수열 점화식도 여러 다양한 방식으로 다시 표현이 가능하지요. 아래 식을 봅시다.
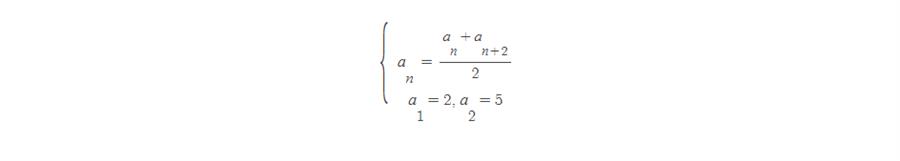
같은 수열을 이번엔 등차중항의 점화식으로 나타내고 있습니다. 그런데 여기서 강한 의구심이 하나 듭니다. ‘일반항으로도 잘만 풀던 수열을 왜 점화식까지 이용해서 귀납적으로 정의하고 있는 거지?’ 새로 배우기 귀찮은데 그냥 일반항만으로 표현하면 안 되는 걸까요? 그건 이 세상에 너무나도 많은 종류의 수열이 있기 때문입니다. 그 여러 수열 중에는 일반항으로 정의하는 것이 오히려 더 복잡하고, 점화식으로 표현하는 게 훨씬 수월한 수열도 많습니다. 세상의 모든 수열을 일반항으로만 표현하는 것이 오히려 더 어려운 일인 겁니다.
예전 교과과정에서는 여러 가지 점화식에서 일반항을 도출해만 하는 경우도 있었습니다. 그러나 지난 교육과정부터는 복잡한 점화식에서 일반항을 도출하는 내용이 대부분 삭제되었습니다. 때문에 현행 교육과정에서 점화식 관련 문항은 다음과 같은 프로세스로 접근하시면 됩니다.
첫째, 해당 점화식이 등차수열이나 등비수열처럼 단순한 수열이라면 바로 일반항을 구해 해결한다. 둘째, 그렇지 않은 경우 항들을 순차적으로 나열하여 규칙성을 찾거나 소거해 문제를 해결한다. 이런 과정을 이해한 후 점화식 문제에 접근한다면 훨씬 수월하게 풀이를 시작할 수 있습니다.

끝으로 수열의 귀납적 정의와 관련하여 교과서에서 단골로 소개되는 탐구 주제를 살펴보겠습니다. 바로 피보나치수열입니다.
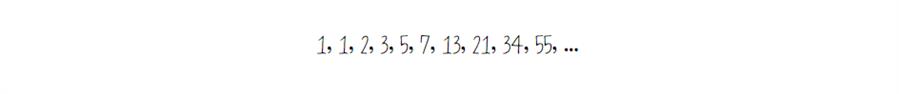
이전 두 항을 합쳐 새로운 항을 만드는 관계의 수열이지요. 즉,
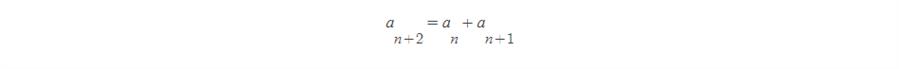
이런 관계를 갖는 것입니다. 수학자 피보나치가 토끼 부부와 토끼 수의 증가 양상을 탐구하다 얻어낸 수열이지요. 피보나치수열은 각항이 자연수이지만 그 일반항은 무리수가 포함되며, 그 극한값은 황금비가 되는 신비롭고 오묘한 수열입니다. 피보나치수열은 교과서 탐구하기 주제 중 시험에 가장 잘 활용되고 있는 내용 중 하나이니, 기말고사 전까지 반드시 정리하고 시험에 임하시길 바랍니다. 날씨가 점점 무더워집니다. 학생들 여러분 모두 건강하시고, 좋은 성적 거둘 수 있도록 오늘도 이지수능교육이 함께 응원하겠습니다!