안녕하세요, 이지수능교육 서포터즈로 활동하고 있는 경희대 의예과 22학번 동규입니다. 먼저 1학기 기말고사 끝난 것을 축하드립니다. 작년에 저 역시 3학년 1학기 시험을 끝내고, 내신 없는 인생에 정말 큰 해방감을 느끼고 행복했던 기억이 나네요. 내신 때처럼 밤을 지새우는 일도 없게 되고 이젠 남은 건 수능과 면접 정도이겠습니다. 고등학교에 입학하여 10번에 내신을 응시하신 분들에게 박수를 보내고 싶습니다. 올해는 9평을 8월 31일에 치러졌습니다. 이번 평가원 모의고사는 수능 전 여러분이 치르던 그 어떤 모의고사보다 중요합니다. 제가 현역일 당시에는 사설기관 모의고사를 신봉하며 이것이 곧 수능 점수다 생각했는데 전혀 아니구요, 9월이 가장 근접하다고 볼 수 있습니다. 사설은 다소 지엽적이고 새로운 시도를 하기 때문에 평가원과는 거리가 있습니다.

작년 입시 결과를 보니 문과 학생들에게 수학은 최저를 맞추는 것에 방해 요소가 되었지만, 최저를 맞추면 거의 백퍼센트 교과 전형에 합격하는 요인이 되었구요, 이과 최상위권 입시에선 수학 1등급 물론이거니 만점은 거진 필수였던 것 같습니다. 그만큼 수학은 정시에서나 수시에서 압도적인 비중을 차지하고 있습니다. 그래서 오늘은 이번 다가올 수능을 대비하는 것과 9모를 응시한 후 어떻게 오답을 할 것인지 다루도록 하겠습니다.

우선 수학 전반에 대한 지금 시점에서의 학습법을 말씀드리고 나서 오답 노트 하는 법을 말씀드리겠습니다. 이과 학생은 대부분 수1, 수2, 미적을 택할 것이고 문과 학생들은 수1, 수2, 확통을 택할 것이기에 이를 기준으로 말씀드리겠습니다. 우선 첫째, 문제풀이 개념을 적립할 필요가 있습니다. 지금 시점에서 잘못된 학습법은 수1, 수2, 미적을 뭉쳐서 양치기하는 것입니다. 문제만 많이 푼다고 수능날 킬러를 다 맞추기 어렵습니다. 작년 수능, 9모, 올해 6모 시험지를 꺼내서 한 번 살펴 보십쇼. 어떤 문제가 출제되었는지, 어떤 유형인지. 문제마다 모두 사용되는 중심 개념이 있습니다. 그 개념을 의도적으로 사용하는 게 바로 수능 수학입니다. 여러분이 생각나는 아무 개념이나 가져다 쓰는 게 아닙니다. 예시를 하나 들겠습니다.

작년 수능 수학 14번 문제입니다. 주어진 함수는 위치함수이지만 주어진 조건은 속도 함수입니다. 이 문제를 보자마자 의도적으로 떠올릴 개념은 미적분 미분 단원에 ‘위치와 속도‘ 파트입니다. 이 문제를 풀 때 항상 속도 그래프를 사용했고, 속도 그래프의 넓이가 곧 이동 거리였다는 것을 기억해낸다면 주어진 위치함수를 곧장 속도함수로 바꾸어 해석해서 풀 수 있습니다. 수학 공부를 하다보면 늘 같은 유형만 반복되고 바뀌는 것은 ’표현‘에 불과하다는 것을 인지하고 있어야 합니다. 이 문제는 속도를 주는 대신 위치로 그래프를 줌으로써 어려워 보이게 출제되었습니다.

둘째로 행동 강령을 정리해라입니다. 문제 조건을 보면 반드시 써야하는 수식이나 원리가 있습니다. 만약 문제를 풀며 틀린 이유가 아이디어 즉, 발상의 부족이었다면 그 발상을 적고 암기하여 발상이 아닌 당연히 해야되는 것으로 만드십쇼. 다음은 그 예입니다.

작년 수능 수학 30번입니다. 역함수 적분을 묻는 문제인데 역함수의 값은 그 어디에도 제시되어 있지 않습니다. 하지만 f함수를 적분하고 이를 역함수 적분 공식에 대입한다면 쉽게 역함수 값을 얻을 수 있는 문제였습니다. 제가 노트에 정리한 역함수 공식은 매우 당연한 것인데, 쉬운 문제가 아닌 30번에서 만났을 때 당황하여 이 개념을 쓰지 못할 것 같아서 노트에 정리하고 외운 공식입니다. 어떤 힘도 들이지 않고 단순 암기 공식으로 문제를 풀기 위함이었습니다. 그 결과 저는 이 문제를 보자마자 풀고 넘길 수 있었고 수능날 수학을 매우 빠르게 다 풀 수 있었습니다. 여러분들도 꼭 문제를 풀고 행동강령을 정립하시길 바랍니다.

셋째로 나눠서 공부하라입니다. 수1을 수열, 삼각함수, 로그지수로 나누어 하루에 한 파트씩 심도있게 개념과 행동강령을 정리하십쇼. 수2 역시 극한, 미분, 적분으로 나누어 공부하세요.

수학 전체를 보면 양이 상당히 많아보이는데 실제로 이렇게 나누어 공부하면 수학 전체를 수십번 반복하고 수능장에 들어갈 수 있습니다.

다음은 9모 수학 오답노트 쓰는 법입니다. 이 역시 제가 위에서 말한 것과 동일합니다.

문제에 사용되는 개념을 지각하고, 행동강령을 떠올릴 수 있게 공책에 적어 암기하는 것입니다. 아래 사진에 보이는 문제는 작년 9모 수학 28번 문제입니다. 사실 현역 9모 수학 때 저 역시 행동 강령이 부족하여 아래 문제를 보고 당연히 해야되는 중심과 원 위의 점 잇기를 하지 않고 진짜로 저 직선의 공식을 구해서 풀려다가 시간을 꽤 많이 소모하여 문제를 풀었습니다. 결국 아래 문제도 삼각함수 도형의 극한에 나오는 대로 삼각함수로 길이만 표현하면 끝나는 문제인데 당연한 개념과 행동 강령을 쓰지 않으니 문제를 돌아가서 풀게 되는 것이었습니다.

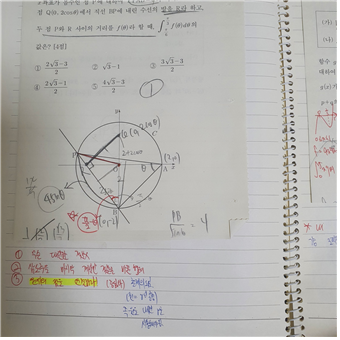
따라서 전 이 문제를 오답 노트하며 중심과 원위에 점잇기, 그리고 당연한 발상 사용하기 등과 같은 말을 적어 이를 암기하였고 그 이후 관련 단원의 문제는 매끈하게 풀 수 있었습니다.

아래 작년 9모 미적 30번 역시 적분 문제였습니다. 작년 수능 30번도 그렇 듯이 말이죠. 조건 가)나)를 차분히 해석하면 쉽게 풀 수 있었지만 마지막 계산이 힘들었습니다. 단순히 치환적분만 하면 답을 구하는 구조였기에 문제를 풀고서 노트에다가 치환적분이라고 적었습니다. 제 풀이 확신을 가지게 함으로써 다음에 만났을 때 확신을 갖고 문제를 풀 수 있기 위함입니다. 오답을 하는 이유엔 개념과 행동강령을 습득하기 위함도 있지만, 수능날 수학적 자신감을 얻기 위함도 있습니다.

여러분이 앞으로 보내게 될 3달의 시간은 여러분의 인생을 좌우할 것입니다. 남은 기간 동안 다양한 모의고사와 문제로 수학적 자신감을 얻으십쇼. 수능까지 준비된 파이널 특강을 활용하거든 이지수능교육 출판 수학 모의고사를 풀거나, 평가원 모의고사를 반복해서 풀어보며 수능날 고득점을 받을 수 있길 바라겠습니다. 이번 수능에선 늘 하던 대로 문제 푸는 순서에 맞추어 최대한 높은 점수를 얻으시길 바라겠습니다. 지금까지 이지수능교육 잉코 동규였습니다.