안녕하세요 이지수능교육 서포터즈 경희대 의대생 '규동'입니다. 3월 모의고사 성적표는 다들 잘 확인하셨나요? 4월에 중간고사도 있으실텐데 3모 성적표도 받고 다가오는 평가원 모의고사까지 생각하셔야 되어서 많이 힘드시겠지만, 끝이 얼마 남지 않았으니 조금만 더 힘내셨으면 좋겠습니다. 이번 6월 모의고사는 6월 1일날 시행되는데요, 중간고사가 끝난 5월 한 달 정도 준비하시고 나면 6월 에 곧바로 치뤄야하니 오늘은 미리 6월 모의고사 대비하는 법에 대해 말씀드리도록 하겠습니다.
규동이의 수학 문제 풀이
작년 수능에선 국어가 쉽게 출제되어 수학을 잘본 경우 정시에서 유리하였습니다. 늘 그렇지만 갈수록 중요해지는 수학, 그래서 6모 대비 중 수학을 다뤄볼 예정인데요, 먼저 6월 모의고사 범위와 시간표를 말씀드린 후 왜 6월 모의고사를 잘 봐야 하는지 어떻게 공부해야 하는지 말씀드리겠습니다.
| 6월 모의고사 범위
|
영역 |
과목 |
출제범위 |
|
국어 |
공통 |
전 범위 (화법과 작문, 문학, 독서, 언어와 매체) |
|
수학 |
공통 |
[수학Ⅰ] 전 범위 [수학Ⅱ] 전 범위 [확률과 통계] Ⅱ.확률 [12확통02-07] [미적분] Ⅱ.미분법 [12미적02-14] [기하] Ⅱ.평면벡터 [12기하02-05] |
|
영어 |
공통 |
전 범위 (영어Ⅰ, 영어Ⅱ) |
|
한국사 |
공통 |
전 범위 |
|
사회탐구 |
생활과 윤리 |
전 범위 |
|
윤리와 사상 |
||
|
한국지리 |
||
|
세계지리 |
||
|
동아시아사 |
||
|
세계사 |
||
|
정치와 법 |
||
|
경제 |
||
|
사회문화 |
||
|
과학탐구 |
물리학I |
전 범위 |
|
물리학II |
Ⅱ. 전자기장 [12물리Ⅱ02-08] |
|
|
화학I |
전 범위 |
|
|
화학II |
Ⅲ. 반응 속도와 촉매 [12화학Ⅱ 03-03] |
|
|
생명과학I |
전 범위 |
|
|
생명과학II |
IV. 유전자 발현의 조절 [12생과Ⅱ 04-06] |
|
|
지구과학I |
전 범위 |
|
|
지구과학II |
Ⅱ. 대기와 해양 2. 대기의 운동과 순환 [12지과Ⅱ05-06] |
| 6월 모의고사 시간표
|
교시 |
시험영역 |
시간 |
|
|
입실 |
오전 8시 10분까지 |
||
|
1 |
국어 |
오전 8시 40분~10시 |
80분 |
|
2 |
수학 |
오전10시30분 ~ 오후 12시 10분 |
100분 |
|
3 |
영어 |
오후 1시 10 분~ 2시 20분 |
70분 |
|
4 |
한국사 |
오후 2시 50분 ~ 3시 20분 |
30분 |
|
탐구1 |
오후 3시 35분 ~ 4시 5분 |
30분 |
|
|
탐구2 |
오후 4시 7분 ~ 4시 37분 |
30분 |
|
|
5 |
제2외국어/한문 |
오후 5시 5분 ~ 5시 45분 |
40분 |
| 6월 모의고사 중요성
6모를 가볍게 생각하실 수도 있을 것입니다. 당장 출제범위도 전체도 아니고 일부인데, 아직 내신 중이라 제대로 대비하지 않아서 6모는 가볍게 보자는 학생이 있을 수도 있습니다. 하지 만 현장에서 시간을 재고 문제를 푸는 모든 모의고사는 정말 중요하고 특히나 이것이 평가원 문제이기 때문에 얼마나 교육청 문항과 결이 다른지 실감 가능한 몇 번 안 되는 기회일 것입 니다.
6모를 대비하는 이유는 궁긍적으로 수능을 잘보기 위함인데, 따라서 먼저 6모와 수능의 유 사도를 직접적으로 말씀드리겠습니다.
6월 모의고사 수학은 수능을 미리 예측해 볼수 있는 아주 좋은 요소입니다. 추상적인 말보다 는 구체적인 예시로써 얼마나 수능을 예측할 수 있는지 말씀드리겠습니다.

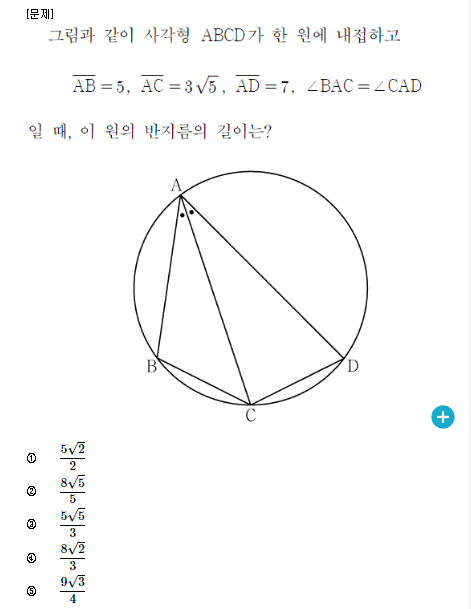
2023학년도 수능 수학 확률과 통계 11번
1. 2023학년도 6모 10번, 수능 11번
두 문항 모두 원이 그려져 있고, 원주각의 성질을 사용해야만 풀 수 있는 문제입니다. 수학1 에서 출제되었는데요. 작년 6모 10번의 경우엔 원의 성질(원주각, 할선, 반지름 길이)을 의도 적으로 꺼내쓰지 못하면 풀기 어려웠습니다. 따라서 6모에 틀렸거나 시간을 많이 소모했다면 이를 제대로 학습하고 수능 때 11번을 푸셨어야 합니다.
이와 마찬가지로 고3즘 되었으면 이젠 감으로 문제를 푸는 것이 아니라 개념를 대입해서 풀어야 합니다. 왜냐하면 모의고사 문제는 내신 문제처럼 어디서 본 문제가 나오는 게 아니라 평가원에서 직접 만들어 출제하기에 처음 보는 문제이기 때문입니다. 이 경우 시간 손실을 최소화하고 바로바로 문제를 풀기 위해선 어떤 형태의 문제에는 어떤 개념을 ‘의도적’으로 써야지 하는 행동 강령을 갖추고 있어야 합니다.


2023학년도 수능 수학 14번
2. 2023학년도 6모 14번, 수능 14번
번호도 같은 위치에 낼 정도로 6모 때 이런 문제를 내겠다고 이미 선전을 한 문항입니다. 14 번 함수 문항 ㄱㄴㄷ 문제는 제작년에도 출제되었고 그해에도 6모, 9모, 수능 같은 유형으로 문제가 출제되었습니다. 여기서 말하는 ‘유형’ 바로 이것이 중요합니다. 바로 위에서 말씀드 린 개념을 ‘의도적’으로 대입하여 푼다와 같은 맥락입니다.
6모와 수능 모두 ‘연속’ ‘극점’과 같이 함수가 가지고 있는 아주 기본적인 요소에 대하여 물어본 문항입니다. 두문항 모두 반 례가 될 수 있는 케이스를 생각해 참 거짓을 낼 수 있었습니다.
수능 14번의 답은 놀랍게도 1번이었습니다. 이 당시 엄청난 논란이 되었는데요. 아주 옛날 기출 문제를 보면 대부분의 ㄱㄴㄷ 문제 답은 무조건 5번일 정도로 5번 답의 비중이 엄청나 게 높았습니다. 또한 단 한 번도 ㄱㄴㄷ 문제의 답이 1번인 적이 없었기에 학생들이 답이 1번이 나왔음에도 1번을 고르지 않고 다른 번호를 골라서 다 풀어놓고 틀리는 상황이 발생했습니다.
이는 22학년도부터 예상가능한 상황이었습니다. 최근 기출 그리고 바로 그해 평가원 을 교과서처럼 여겨야하는 이유가 바로 이것입니다. 문제 유형뿐만 아니라 이와 같은 돌발상 황까지도 대비할 수 있습니다. 작년 6모 14번의 답은 4번이었습니다. 제작년에는 3번이었습 니다. 이와 같이 22학년도부터 ㄱㄴㄷ 문제의 답을 5번으로 내지 않았다는 것을 염두하고 수능장에 갔으면 1번이 나왔을 때 고민 없이 1번을 고르고 넘길 수 있었을 것입니다.


3. 2023학년도 6모 15번 수능 15번
이 문제 역시 평가원에서 6모와 같이 내겠다고 선전을 한 문항입니다. 6모, 9모, 수능 모두 15번 문항에 수열을 출제했습니다. 두 문항 모두 확정되지 않은 수열을 제시하고, 직접 여러 가지 케이스 중에서 조건에 부합하는 수열만 찾으면 되는 문항이었습니다.
귀납적으로 수열을 추론하는 문제로 수1 수열의 대표 유형입니다. 보자마자 우선 이 수열을 어떤 원리로 항이 나열되는지 이해했으면 쉽게 답을 낼 수 있었을 것입니다. 6모 때 만약 이 문항을 보고, 손 도 쓰지 못하고 처다만 보고 끝난 학생이라면 이때 반드시 ‘다음에 수열 케이스 찾는 문항이 나오면 우선 항을 나열해보고 원리를 파악해야지’와 같은 행동강령을 만들었다면 수능날 전혀 당황하지 않았을 것입니다.


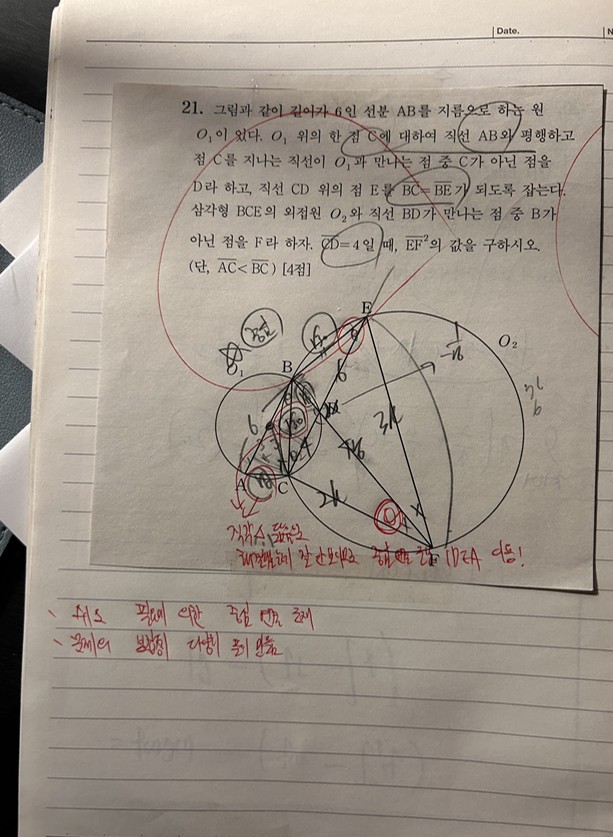
2023학년도 수능 수학 21번
4. 2023학년도 6모 21번 수능 21번
이 문제 역시 대놓고 연계한 문항입니다. 6모 21번은 로그가 정수가 될 때 문제이고 수능 21 번은 로그지수가 정수가 될 때의 상황에 대해 묻는 문제입니다. 심지어 두 문항 모두 ‘모든 자 연수의 합을 구하시오’ 문제로 답이 될 수 있는 상황에 부합하는 모든 숫자를 더하는 문제입니다. 이런 문제가 출제되면 학생들은 자연스럽게 혹시라도 숫자 하나를 빼놓고 답을 구할까 봐 심리적으로 불안하기 쉽습니다.
따라서 6모 때 이문제가 어려워만 보이지 실제로는 답이 되는 자연수 처음과 끝 경계값만 명확하게 확인하면 틀리지 않는다는 행동강령만 만들었다면 아무 문제 없이 풀 수 있었을 것입니다. 이렇게 공통문항에 대해서만 연계되는 정도를 말씀드렸습니다. 선택 문항을 포함한다면 더 많은 연계가 됩니다.
| 6월 모의고사 대비법
사실 위에서 6모와 수능의 연계 정도를 말씀드리며 미리 대비법을 말씀드렸습니다.

1. 개념을 의도적으로 대입해라
문제는 늘 처음 보는 문제일 것입니다. 시험장에 들어갔을 때 긴장감, 그리고 1교시 국어로 잘 돌아가지 않는 머리 상태 등을 고려하면 느낌적으로 문제를 푼다면 어떨 때는 잘 풀 수 있겠지만, 또 어떨 때는 잘 안 풀릴 것입니다. 따라서 문제를 보았을 때 당연히 이 개념을 의도 적으로 적용할 수 있게 연습하세요.
다양한 문제를 푸는 이유는 몰라서 배우기 위해 푸는 것이 아니라, 상황에 맞는 개념을 의도적으로 쓰는 연습을 하기 위함입니다. 미분가능, 합성함수 함수추론, 삼각함수 도형의 극한 등을 떠올려 보세요. 어떤 개념을 써야하는지 분명 정리하고 익혔을 것입니다. 이제 익힌 개념을 자연스럽게 적용할 수 있도록 문제를 많이 푸셔야 합니다.
더이상 내신 문제로 연습하는 게 아닌, 평가원 기출, 사설 수학 문제 등을 활용하세요. 저 역시 이지북스 출판 이지핏 모의고사 final를 막판에 풀었습니다. 기출이 외워질 정도로 푸셨다면 다른 문제들로 실력 점검을 받아보세요.
규동이의 수학 문제 풀이
2. 행동강령을 만들어라
개념을 의도적으로 대입하는 것도 행동강령의 일종이지만, 시험장에서 태도에 대한 것까지 도 만드셔야 합니다. 시험 끝나고 누구나 문제 순서를 다르게 풀 걸, 그냥 건너뛰고 문제를 풀 걸 이런 생각을 많이 하셨을 겁니다. 게다가 이젠 11번부터 어려운 문제가 출제됩니다.
작년 수능 등급컷은 84점이었습니다. 이 말은 즉, 모두 다 어려워한다는 것입니다. 84점 이상 이면 1등급인 시험에서 어떻게든 1등급을 받아야한다면 선택과 집중이 필요합니다. 다 맞아야 대학을 가는 게 아닌, 최대한 높을 점수를 받아 지원하는 대입 체제에서 본인이 연습을 통해 어떤 문제를 순서로 풀 것이며, 몇 분 이상 시간을 들였는데 풀지 못하는 문제는 버려야지 이런 생각들을 미리 해두십쇼.
당황하면 시험은 망합니다. 모두 예측된, 통제된 상황들이 될 수 있도록 미리미리 준비하시길 바랍니다.
단기간에 6월 모의고사 대비가 어렵게 느껴지시는 분들은 제가 다녔었던 이지수능교육에서 6모 대비를 위해 이지웨이 수업이 진행된다고하니까 알아보시길 추천드리며 마무리하겠습니다
여러분 모쪼록 이번 중간고사 그리고 다가오는 6월 모의고사 준비 잘하셔서 원하는 결과 있으시길 바랍니다. 지금까지 잉코 규동이었습니다. 감사합니다.