안녕하세요 여러분 저는 차의과학대학교 약학과에 2학년으로 재학 중인 잉코 아이입니다! 어느새 2024학년도 수능도 마무리되고 한 해도 슬슬 끝을 보이는 것 같습니다. 다들 수능은 어떻게 치셨나요? 과거를 통해 배울 것들만 배우고 자신을 그를 통해 고쳐나가는 것이 더 중요할 거라 생각합니다. 따라서 오늘 칼럼은 올해의 수능, 그 중에서도 수학 과목을 다시 돌아보며 올해 수능 문제의 출제 경향성이 어떠했는지와 킬러문항 22번, 30번 그리고 앞으로 이를 대비해 어떻게 공부하면 좋을지에 대해 글을 써보려 합니다. 그럼 칼럼 시작하겠습니다!
| 2024학년도 수능 난이도
올해의 수능은 전체적으로 불수능이라는 얘기가 많았죠. 사실 등급컷을 보아도 이 점을 잘 알 수 있을 것 같습니다. 수학, 그 중에서도 미적분의 1등급컷이 81~85점이라고 예측됐다고 하는데요.
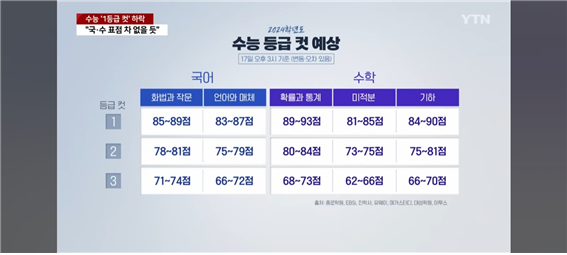
출처 - YTN
요즘의 수학 등급컷들이 90점을 넘기는 경우가 많지 않긴 하지만 아무리 그래도 이렇게 80점대 초반으로 1등급컷이 형성되는 것은 역대 수능들과 비교해 봐도 이례적인 일 같습니다. 그만큼 학생들이 올해 수학을 어려워했다는 것이겠죠.
그렇지만 정말 올해 수능 수학 문제가 무자비하게 어렵게 출제가 되었느냐라고 물으신다면, 저는 죄송스럽지만 아니라고 대답하고 싶습니다. 저도 수능이 끝나고 등급컷이 굉장히 낮은 것을 보고 곧바로 수학 문제를 풀어보았지만, 만약 기초 실력을 탄탄하게 해두고 기본 개념을 잘 잡아뒀다면 학생들이 보다 잘 풀 수 있지 않았을까 생각합니다.
| 미적분 문제 분석과 풀이
그럼 지금부터 수학 문제들, 그 중에서 미적분에 초점을 맞추어 하나하나 분석해면 서 이렇게 생각한 이유를 말씀드리도록 하겠습니다.
가형, 나형의 수학이 사라지고 올해는 심지어 킬러 문항 배제까지 합해지면서 수능 수학은 점점 경향성이 바뀌고 있습니다.
예전에는 21, 29, 30번 등의 문제에 어려움을 최고치로 넣고 나머지들을 쉽게 출제했다면. 이제는 점점 이러한 킬러문제들의 난이도를 낮추고 대신 그 난이도를 다른 여러 문항들로 분배해서 준킬러 문항들을 다량 출제합니다. 이번에도 이와 비슷합니다.
22, 30번 등의 오답률이 높은 문항이 있긴 하지만 전체적으로 난이도가 평균을 약간 넘기는 수준인 문제들이 주로 출제되었기에, 만약 기초 실력을 탄탄하게 하고 여러 유형들을 접해보았다면 보다 쉽게 풀 수 있었을 것입니다.
그렇다면 22, 30번 등의 오답률이 높은 유형은 어떻게 접근했어야 할까요? 이는 하나씩 살펴보도록 하겠습니다.
| 수능 수학 22번 풀이
먼저 22번부터 보자면 비교적 조건이 간단히 나와있다는 느낌을 받을 수도 있지만 생각보다 조건들에서 알아낼 부분들이 많습니다. 우선 최고차항 계수가 1이고 미분계수 값이 음수인 부분이 존재하기에 삼차함수가 두 번 꺾였을거라는 개형과 x=0의 위치(감소구간)를 알 수 있습니다.

수학 문제는 항상 나와있는 조건을 전부 사용해야 하기에 남은 조건들을 살펴보면 이제 결국엔 박스 안에 있는 조건을 해석하는 것이 중요할 것이라 느낄겁니다.
박스 안의 조건을 계속 보면 k-1과 k+1이 들어갔으니 x값이 무려 2씩이나 간격이 남에도 둘의 함숫값의 부호 곱이 –는 절대 안 나온다는 점에서 단순한 통과의 양상보다는 x축과의 교점이 정수점이 되면서 이러한 x축 경계점에서의 부호를 상쇄시켜주지 않을까 하는 걸 추측 가능하며 x축과의 교점들 간의 간격이 너무 크면 안될 것 같다고 생각할 수 있습니다(경계점의 수가 늘어나므로).
그에 따라 될 수 있는 개형들을 x축의 위치에 따라 케이스 분류해 보면 우선 부호 변화 지점이 가장 적으면서 교점은 많은 한점에서 x축에 접하는 케이스부터 생각해 볼 수 있습니다. 하지만 이를 계속 해보다보면 중간에 있는 x=0이라는 값 때문에 이것이 성립하기 쉽지 않은 걸 알 수 있을 겁니다.
따라서 남은 케이스는 교점이 하나 또는 세 개인 케이스인데 교점이 하나인 케이스는 교점이 아무리 정수점이라고 해도 성립이 절대 불가능할 것입니다(단순한 통과의 양상이므로). 따라서 교점이 세 개인 케이스를 바로 생각해 보고, 교점이 최대한 정수점으로 구성되게끔 t, 0, 1 혹은 –1, 0, t라는 교점을 가지는 두 케이스에서 각각 조건으로 나와있는 미분계수 값을 활용해 남은 교점 t값을 알아내고 한 가지 케이스만을 남길 수 있습니다.
따라서 결국에 22번의 핵심은 박스 안의 조건을 잘 살펴보면서 유의해야 할 점들을 기억하고 이후부터 개형 케이스 분류를 하며 그래프의 개형을 찾아내는 것입니다. 케이스 분류는 항상 어려운 수학 문제들에서 꼭 사용되는 기법이므로, 평소에 개형의 가능성을 찾는 케이스 분류 연습을 많이 했다면 보다 수월하게 풀 수 있는 문항입니다.
하지만, 이번 수능 수학 문항 중 가장 시간이 오래 걸리고 난이도도 높은 문제였던 건 사실이기에 마지막 순서에 풀었다면 더 좋았을 듯 합니다.
| 미적분 30번 풀이
다음으로는 미적분 30번입니다. 사실 기본 개념만 잘 되어있다면 5분 안에도 풀 수 있던 문제라 제 생각에는 아마도 다들 30번이라는 번호에 겁을 먹어 못 푼 게 아닐까 싶은데요.

h(x)가 x=a에서 극대, 극소를 가진다는 조건 하나만이 나와있으므로 이를 해석하면 되는데 h(x)를 미분해 보면 이 조건은 곧 x=a에서 f(x)와 g(x)의 대소가 바뀐다는 걸 말하고 싶다는 걸 알 수 있을 겁니다.
그리고 여기에서 접선을 그었는데 접점에서 대소관계가 바뀐다는 것에 의문을 가지고 이것이 될 수 있는 케이스, 즉 변곡점에 대해 떠올려봐야 합니다. 변곡점에서의 접선은 일반적인 접선들과는 달리 함수를 통과하는 듯한 양상을 보이므로 결국 이는 x=a가 f(x)의 변곡점이라는 정보를 주고 싶었던 것이죠.
문제에서 f’(x)가 제시되어 있으니 이를 미분하고 부호 변화 지점을 본다면 쉽게 a값들을 찾을 수 있을 것입니다.
따라서 30번은 변곡접선이라는 함수 기초개념을 잘 배워뒀는지를 확인하는 문항이었습니다.
| 마치며
수학을 공부할 때 흔히들 학생들이 당장에 시험이 얼마 안 남아서 어려운 문제들만 골라서 풀고 유형별로 그저 풀이를 암기하는 데에 집착을 하는 경우가 많습니다. 하지만, 당연하게도 수학은 이처럼 기본 개념을 잘 알고 있어야 어려운 문제들도 풀 수 있습니다.
우리가 흔히 킬러 문항이라고 부르는 것들도 우리의 교육과정에서 벗어난 것을 내는 것이 아니라 얼마나 개념을 세밀하게 잘 이해하고 있고 이 문제가 어떤 개념과 관련된 것인지를 파악하는 능력을 보고 싶은 문항들이니까요.
위의 정보들을 바탕으로 볼 때 올해의 수능 수학은 여러 유형들에 대한 기초적인 실력과 기본 개념 이해, 케이스 분류 능력과 같은 경험을 요구했다고 할 수 있습니다. 그리고 이는 꼭 올해 수능 수학만 그랬던 것은 아니며 지금까지의 대부분의 수능 수학들이 공통적으로 요구하는 능력이 아닐까 싶습니다.
따라서, 때로는 문제를 잘 푸는 것도 중요하지만 자신이 정말 함수나 지금 배우는 내용들에 대해 헷갈리는 부분 없이 명확하게 이해하고 있는지를 점검하는 것도 굉장히 중요할 것 같습니다. 처음에 말씀드렸듯 지나간 과거에 미련을 가지는 건 시간을 허비하는 일이라고 생각합니다.
그래서 긴 글이 되긴 하였지만 오늘 칼럼을 잘 보시고 올해의 수능을 떠올리며, 자신이 고쳐야 하는 부분들을 찾고 개선해나가는 데에 시간을 쓰시면서 앞으로 나아가시면 좋겠습니다. 항상 응원하겠습니다. 감사합니다!