여러분들은 세특이 갖는 의의가 무엇이라 생각하나요? 어떤 세특이 속히 말하는 '좋은' 세특이라고 할 수 있을까요? 혹은, 이를 통해 '무엇'을 강조하고 싶나요?

보통 세특을 통해 강조하는 사항은 인성과 전공 적합성이라고 생각합니다. 대부분은 인성은 비교과 영역(자율, 동아리, 진로 등), 전공 적합성은 교과 영역에서 드러낼 수 있다고 생각하는 것 같아요. 그렇지만 교과 세특에서도 둘 다를 충분히 강조할 수 있다고 생각합니다. 저는 특히 수학에서 두 가지를 모두 강조했는데, 제 수학 세특은 어땠는지 살펴보러 갑시다!

| 인성적 측면 강조하기

교과 세특에서 인성적 측면을 어떻게 강조할 수 있을까요? 보통 성실성과 리더십이라 생각해요. 그리고 저는 1학년 때 수학에서 이를 활용한 적이 있었답니다.

첫째는 교과서 문제 풀기 및 모의고사 오답노트 쓰기였어요. 사실 코로나 때문에 등교를 못 하던 상황에서 숙제로 나왔던 거였는데, 나중에는 한 사람들만 세특에 적어주는 것으로 바뀐 기억이 납니다.

이 사진은 1학년 수학 세특인데요, 학술적인 내용보다는 인성적인 면이 강조되어 있습니다. 저는 1학년 때 희망 진로가 수학이었어서, 수학 선생님 붙잡고 매시간 질문했던 기억이 나네요.

단순히 문제 풀이 방법을 질문한 것이 아니라, 수업 시간에 배운 개념에 대해서 질문했어요. (ex. 귀류법에서의 부분집합 성립 유무 등) 그래서 ‘순수한 탐구심’, ‘자기주도적 학습태도’등이 적혀있는 것 같아요.

| 전공적합성 어필하기

이 부분은 추후 대입에서도 사용했습니다. 저는 세특 등에서 수식을 쓸 때 직접 계산하고 증명하는 것에 집중했어요. 그래서 자소서를 쓸 때도, 단순히 이 내용을 조사했다는 사실에 그치지 않고 수학적으로 유도했다고 전공 적합성을 어필했습니다.

저는 고등학교 2학년 때 지금의 진로를 결정했는데요! 그래서 본격적으로 지구과학 관련 내용으로 꾸려 나갔습니다.

1학기에는 지수&로그 단원에서 '거리에 따른 별의 밝기를 계산'하는 방법을 조사했어요. 이는 지구과학 1에서 나오는 포그슨 방정식과도 연관이 있어서, 교과 융합으로도 적합할 것 같아요.

위 사진은 관련 내용을 발표하면서 만들었던 발표 자료입니다. 사진으로 포그슨 방정식을 유도하는 것을 선택했는데, 이외에도 연주 시차, 거리 공식 등을 활용하는 방법에 관해서도 소개했어요. 사진 부분은 사실 지구과학Ⅰ에서 그대로 나오는 내용인데, 교과 간 연계성을 찾는 것만 해도 큰 의의가 있다고 생각해요 :)

2학년 2학기엔 지구과학 중에서도 지구물리학에 흥미가 생기기 시작했어요. 그래서 수학에서도 관련 내용을 소개하기로 했습니다. 주제는 '미분으로 스넬의 법칙 유도하기'였어요. 스넬의 법칙은 물리1에서도 나오는 내용이지만, 이를 미분으로써 직접 증명하는 것은 나오지 않아 직접 해 보았습니다. 또한 이를 활용하여 알 수 있는 지구물리학적인 특징까지 분석해 보았어요.

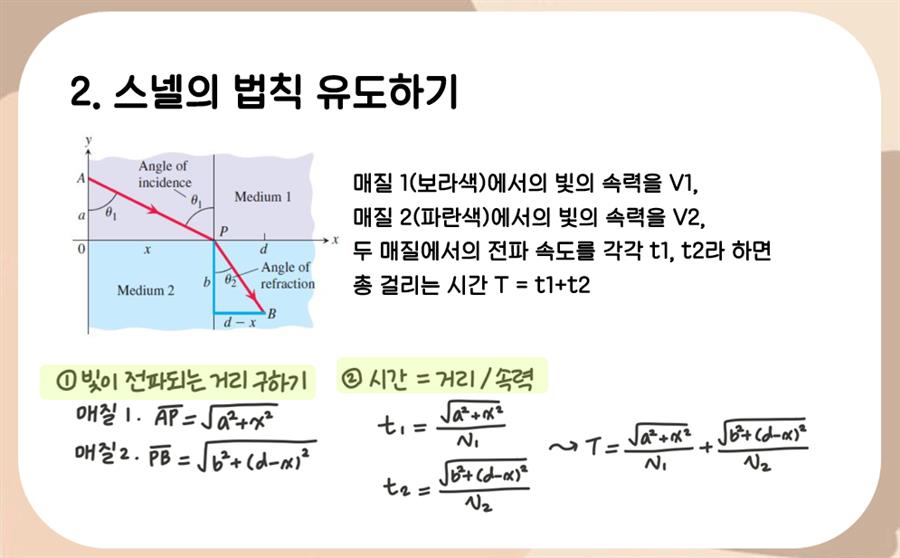
사진은 제가 직접 스넬의 법칙을 유도하여 발표했던 자료입니다. 고3 미적분 내용을 활용하기는 하지만(합성함수의 미분), 뒤에서 일반화된 합성함수의 미분법을 언급하고 유도했습니다. 대신 수학2이기 때문에 미분으로써 유도할 수 있다는 사실에 초점을 두었어요.

저는 고등학교 2학년 여름방학에 미적분 예습을 진행해서, 당시에 이해하고 작성했던 내용입니다. 여러분 중에서도 해당 주제를 채택하고자 한다면 미적분 과목에서 하는 것을 추천합니다.

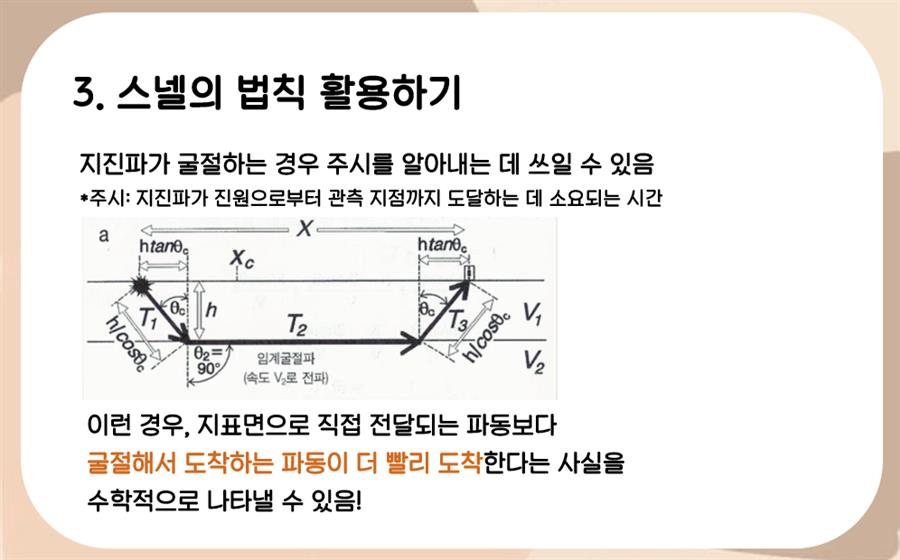
이 사진은 위 공식으로써 유도할 수 있는 과학적 의의를 작성해 둔 것입니다. 단순히 생각했을 때 굴절파는 직접파에 비해 이동 거리가 길어 늦게 도달할 것 같은데, 스넬의 법칙에 의하면 일정 거리 이상부터는 굴절파가 더 빨리 도달함을 알 수 있습니다.

이 내용은 대학 진학 후 지구물리학 전공에서도 공부했던 내용이에요. 그래서 전공 적합성을 어필하기에 너무나 좋은 세특이었다고 생각합니다.

고3 때는 교육과 수학 세특을 연결하기로 생각했어요. 모학문(지구과학)에 대한 전공 적합성은 충분한데 교직에 대해서는 부족하다는 피드백을 들었거든요.

첫 번째로 한 건, 경제수학에서 '교육의 정도와 경제성장 정도의 연관성'을 조사하여 발표했던 것이었어요. 경제학 분야에선 식견이 짧아 당시에는 관련 논문 내용을 중점으로 소개했던 기억이 납니다.

한국의 현 상황에 대해서 분석한 논문을 추가로 찾아서 함께 발표했어요. 한국에서는 교육에 대한 투자에 따른 인적 자본이 충분히 생산되지 않고 있음을 자료를 통해 보여주면서, 교육 거품 현상에 대해서 설명했던 기억이 있습니다.

두 번째로 한 건, 확률과 통계 세특에서 '드레이크 방정식을 이용하여 구한 내가 지구과학 교사가 될 확률'을 구해서 발표했던 것이었어요. 확률의 독립의 성질을 활용하여, 교사가 되기까지의 과정을 조사하고 이를 확률로써 나타내 보았습니다.

결괏값은 1.12%였는데 실제로 그 정도로 희박하진 않을 거라 믿어요...ㅎㅎ 여러분도 확률과 통계를 듣는다면 자신의 진로와 연관하여 한 번쯤은 해 보시길 추천합니다!

제가 이렇게 인성과 전공적합성 어필에 도움이 되는 활동들은 이지수능교육의 생기부컨설팅 선생님께서 많이 알려주신 덕분에 더욱 빛나는 생기부를 완성할 수 있었다고 생각해요! 여러분도 생기부를 어떻게 꾸려가야 할 지 막막할 때 이지수능교육의 생기부 컨설팅 수업이 많은 도움이 될 것이라고 믿습니다.

이상으로 제가 고등학교 3년간 작성했던 수학 세특을 되돌아보는 시간이었습니다. 여러분들은 어떤 진로를 위해 꾸려나가고 있나요? 제 예시가 여러분들의 세특 부담 경감에 큰 도움이 되었길 바라며, 이만 줄이겠습니다 :)