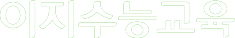혹시 3월 모의고사는 큰 문제없이 잘 보셨나요? 어찌 됐든 ‘수능 준비’라는 긴 레이스를 대비하는 데에 있어서 3모는 큰 고개가 아니니 오래 머무르고 계시면 안 됩니다.

저 또한 그랬듯이 학생들은 시험을 앞두고 그 시험에서 이루고자 하는 목표를 설정합니다. 열심히 노력했더라도 그 날의 컨디션, 시험지 스타일에 따라 목표의 성취 여부가 달라질 수 있겠습니다.

그중, 목표를 이루신 분들은 정말 축하합니다. 새로운 학년을 맞이하며 첫 시험을 완벽하게 소화한 여러분들은 그 기쁜 마음을 원동력으로 다음 고개를 넘고자 해야 할 것입니다.

그렇지 않으신 분들도 계실 겁니다. 성적은 좋아도 더 높은 꿈을 이루기엔 아쉬운 케이스, 스스로 생각하기에 노력 대비 성적이 아쉬운 케이스 등 사실 대다수의 학생은 목표 달성에 실패합니다. 그렇기에 3모가 수능이 아닌 것에 안심하면서 부족한 부분을 메꾸기 위한 공부가 필요할 것입니다.

작년의 저도 언어와 매체/미적분/화학1/생명과학1을 선택해 3모를 치렀습니다. 언매, 미적 선택은 고민하지 않았지만 과탐 선택을 앞두고 고민이 깊었습니다.

내신으로 물리학1/화학1/생명과학1을 공부하던 저는 화1, 생1이 주는 시간적인 압박을 고려하여 둘 중 한 과목을 제하려 했으나 물1의 3단원(파동)이 저에게 알레르기를 일으키는 것만큼 와닿지 않아 화생조합을 과탐 선택했습니다.

분명히! 이러한 케이스의 학생이 있을 것이며!! 그 친구들이 도움이 필요할 것이라 마음대로 생각한 저는!!! 수능 화생 만점자로서 조언을 몇 가지 드리고자 합니다.

화학1은 과탐 중 가장 적은 개념량을 자랑합니다. 생1의 개념량도 적진 않으나 지구과학, 사회탐구 과목과 비교해 볼 때 무난합니다.

그런데 시험지 구성을 떠올려보면 화학1과 생명과학1은 [개념형 13Q + 추론형 7Q] 의 꼴로 이루어져 있음을 알 수 있습니다. ‘쉬운 문제가 많구나!’라고 생각하는 것이 아닌, ‘개념을 100% 정복해야 한다!’라고 느끼셔야 합니다.

13문제 중 분명 수험생의 허를 찌르는 문제가 있을 것이며 그 문제를 틀리는 것은 남들보다 추론형 문제 하나를 더 맞혀야 원점이 될 수 있음을 의미합니다.

안타깝게도 많은 학생들은 수능이라는 큰 산 바로 앞에서까지 등산화, 비상약같은 필수품(개념형 문제)를 챙기지 않아 하산하게 됩니다. 0점에서 80점이 되는 기간이 80점에서 100점이 되는 기간보다 짧은 것처럼, 개념형 문제를 100% 정복하기 위한 시간을 투자할 수 있길 바랍니다.

과탐 선택자들이 겪게 되는 가장 안타까운 상황은 무엇일까요? 당연히 수능 시험장에 지각하는 등의 놀라운(?) 경우를 제외하고 생각해면, 역시 문제를 풀 실력이 있지만 시간이 부족한 경우일 것입니다.

이는 과탐이 30분이라는 짧은 시간동안 20문제를 ‘계산’하고 ‘추리’하는 능력을 요구하기 때문입니다. 특히 이러한 점은 화1, 생1에서 심해지는데 저는 재밌게도 화학적, 생명과학적인 방법으로 타임어택 문제를 해결했습니다.

대뇌와 소뇌의 관계성을 떠올려봅시다. 중추신경계의 중심기관으로서 대뇌는 까다로운 문제들을 풀어나갑니다. 당신의 대뇌는 실수할 수도 있고 문제 자체의 해석에 실패할 수도 있습니다.

여기서, 특히 ‘실수’를 할 때, 당신의 뇌는 그것을 ‘오류’라는 데이터로 입력합니다. 소뇌는 ‘퍼킨제 뉴런’을 활용해 ‘오류’를 일으키는 근육을 막기 위한 억제성(GABAergic) 신호를 심부핵에 보내면서 오류라고 불리는 실수를 줄일 수 있습니다.

자잘한 실수를 줄여나가고, 익숙한 문제들을 더 빠르게 해결해나가면서 자연스레 시간이 넉넉하게 남아있음을 확인할 수 있습니다.

쉬운 문제지만, 분명 ‘소수’가 들어간 계산을 싫어하는 학생들은 살짝 화가 났을지도 모릅니다. 저 또한 그런 학생인지라 어떻게든 소수를 회피할 수 있는 방법이 있을까하고 문제에서 ‘구하고자 하는 값’을 확인해보니 x와 y의 비율을 구해야 함을 알게 되었습니다.

즉, 0.1과 0.3이라는 값 자체는 아무런 의미도 없습니다. AC2와 B2C의 질량의 ‘비’를 구하기 위해선 그저 A2B4와 C2의 질량비를 활용하면 됩니다.

저는 상황을 단순하게 보기 위해 각각 1g, 3g이 있다고 생각하고 위의 원자량 비 조건과 함께 생각하여 계산을 더 쉽게 하기 위해 8을 곱해 8g, 24g있다고 생각하며 간단히 풀었습니다.

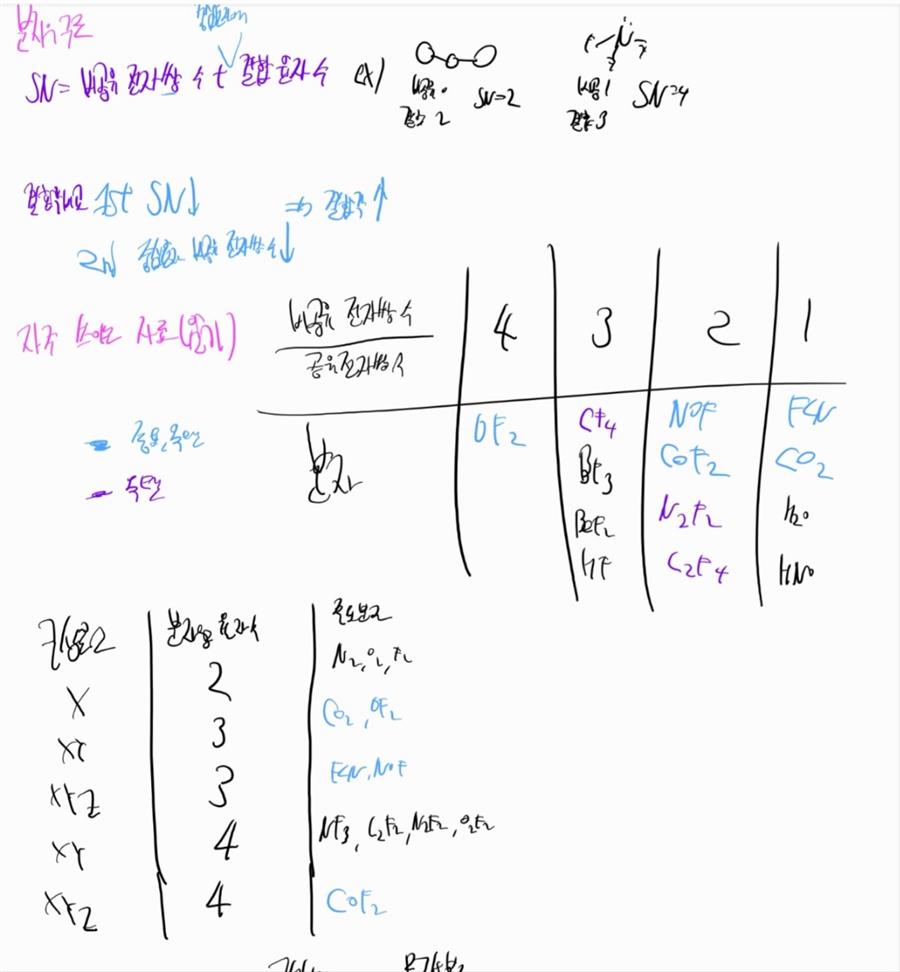
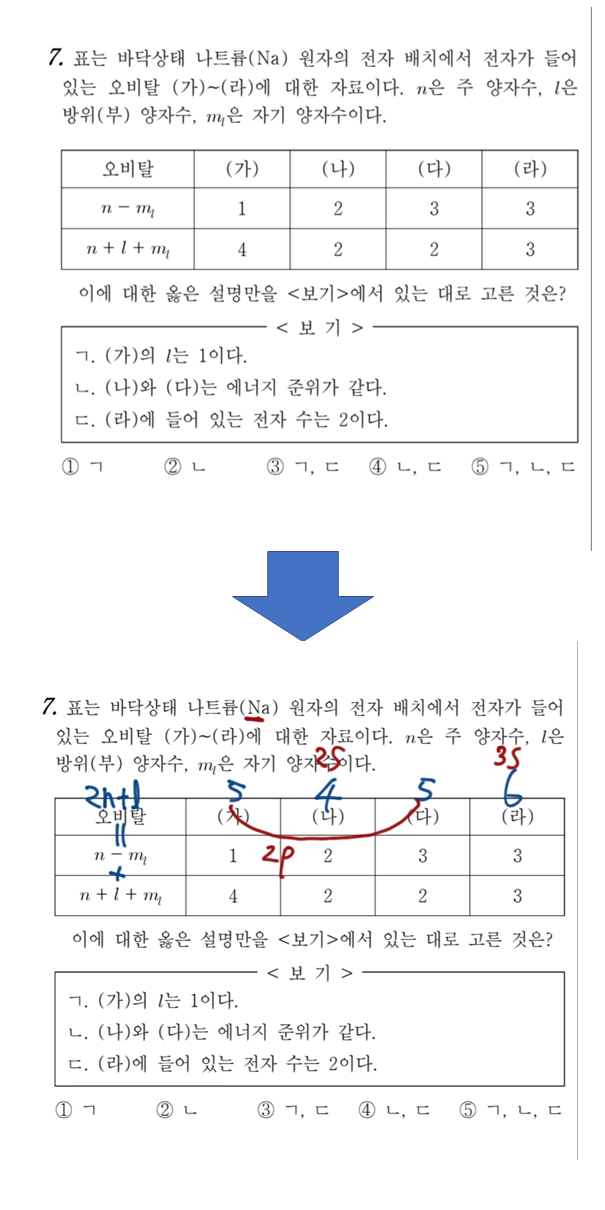
오비탈 문제 연습이 미숙한 학생한테는 조금 당황스러울 수도 있었던 문제입니다. (가), (나), (다), (라)가 각각 무슨 오비탈인지도 모르겠는데 자기양자수를 물어보니 머리가 뜨거워짐을 느낄 수도 있겠습니다.

저는 표의 2행에선 자기 양자수에 음의 부호가, 3행에선 그것에 양의 부호가 있다는 점에 주목했습니다. 방금 말했다시피 자기 양자수를 다루기가 까다로웠는데 그냥 그것을 없애버리면 해결되는 문제입니다. 따라서 저는 2행과 3행을 더해버리는 식으로 보기 쉽게 표를 정리했습니다.

2n+l의 값에 따른 오비탈이 하나씩 정해져 있다는 것을 이용해 금방 숨겨져 있는 오비탈의 정체를 밝힌 것입니다.

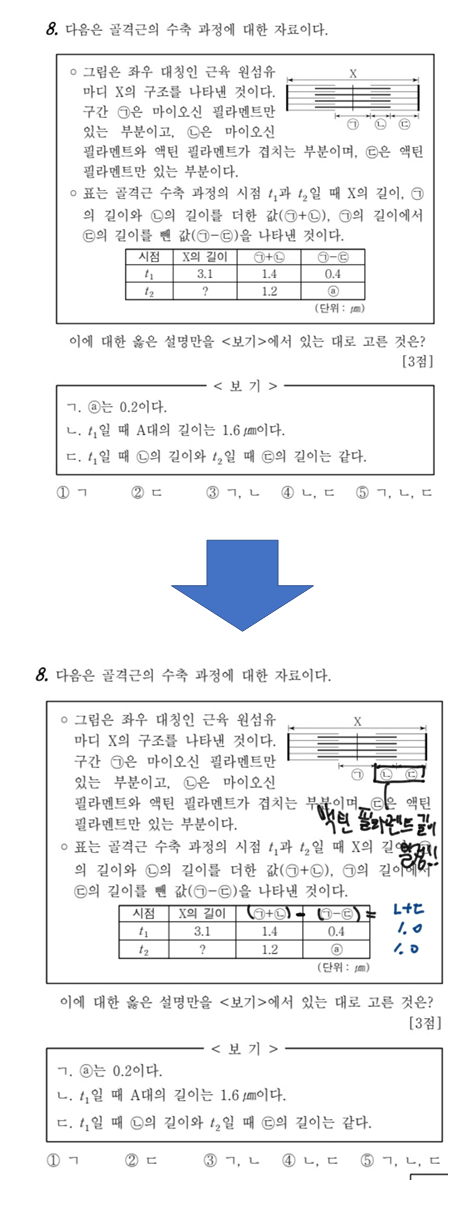
생명과학1의 흔한 근수축 문제입니다. 근수축 문제에선 변하지 않는 값(상수)에 주목하며 조건을 해석하는 것이 기본적인 자세라고 할 수 있겠습니다. 예를 들어, 필라멘트의 길이가 일정할 것이며 문제에선 ㄴ+ㄷ의 길이가 일정할 것입니다. 자료를 보니 3열에서 4열을 빼고 싶어집니다. 즉 ㄴ+ㄷ = 1.0임이 항상 성립함을 알게 되어 a값을 구할 수 있고 순조롭게 문제가 풀립니다.

이런 식의 숫자, 자료를 조작하는 능력 역시 수많은 문제풀이경험을 바탕으로 하는 만큼 2번에서 강조한 양치기가 또 저희한테 도움의 손길을 내어주네요.

위 내용들을 요약하면

1. 개념

2. 양치기

3. 조작

이 세 가지를 기억하면 화학1, 생명과학1 등 과탐 선택 과목들을 정복할 수 있습니다. 추가로 어려운 문제, 심리적인 좌절 등의 고난을 겪게 되더라도 그것을 꺾고 일어날 수 있는 마음이 중요하겠습니다.

더불어, 혼자서 과탐 선택 과목을 공부하는 게 어렵다면 전문가의 도움을 받을 수도 있는데요. 저 역시 이지수능교육 1:1 맞춤 과외를 받아 수능 최저를 맞춰 의대에 합격할 수 있었습니다.

이지수능교육 과외에 대해 자세히 알고 싶으신 분들은 아래 버튼을 클릭해주세요!

이쯤 칼럼 마치도록 하겠습니다. 오늘도 좋은 하루 보내시길 바랍니다. 긴 글 읽어주셔서 감사합니다! THANK YOU!